F12 Update - Presentation at IAC 2023

I attended the 2023 International Astronautical Congress in Baku, Azerbaijan last week and presented my updated paper (published in the conference proceedings) Morphology of Polyhedral Space Habitat Modules - Identifying the Ideal Form Using Multi-Criteria Analysis. This paper describes the results of my research into determining the most-ideal polyhedron to select when designing polyhedral space habitat modules. The surprising result of the research (described in the paper and in the slideshow below) not only confirmed that the Rhombic Dodecahedron is the most ideal form among those studied, but also illustrates that it is effectively unbeatable by any other polyhedron, no matter what factors one thinks are most important.

Hello. My name is Elliott Orion Ruzicka, and I'm a registered architect operating out of New York City.

Shape matters. If there is anyone here that doesn't agree that this applies to space habitat design, it is my hope that by the end of this presentation they will think differently. It is also my hope that the results I will be presenting at the end will surprise and possibly even shock you.

The concept of polyhedral space habitat modules has been explored in prior research by Frisina, de Weck, Howe?, and Ekblaw. While these studies present arguments supporting certain candidate polyhedra based on desirable qualities, little in the way of rigorous evaluation has been dedicated to determining the most ideal polyhedron among many candidates by way of employing many consequential evaluation metrics.

The aim of this study was to determine as close to objectively as possible which polyhedral form is the most suitable to the application of space habitat modules. Although this study was not absolutely exhaustive, it stands as the most comprehensive evaluation of its kind at the time of publication. Furthermore, it presents a novel conclusion that has not been considered by other researchers. This is an important question to answer sooner rather than later, as work to create polyhedral space habitat modules is currently ongoing, and due to first-mover advantage the first shape used is likely to set a standard early on, and any disadvantages will be perpetuated.

In this presentation, I will be covering which candidate polyhedra were selected, which metrics were used to evaluate the candidate polyhedra, what analysis methodology was used to process the raw metric values, and finally I will be presenting the results.

This is the abbreviated version of the candidate polyhedra selection criteria. I'd be happy to discuss these at a later time. All said, (10) polyhedra were selected. The final candidates are as follows.

The Tetrahedron, composed of (4) regular triangles.

The Cube, composed of (6) squares.

The Octahedron, composed of (8) regular triangles.

The Dodecahedron, composed of (12) regular pentagons.

The Icosahedron, composed of (20) regular triangles.

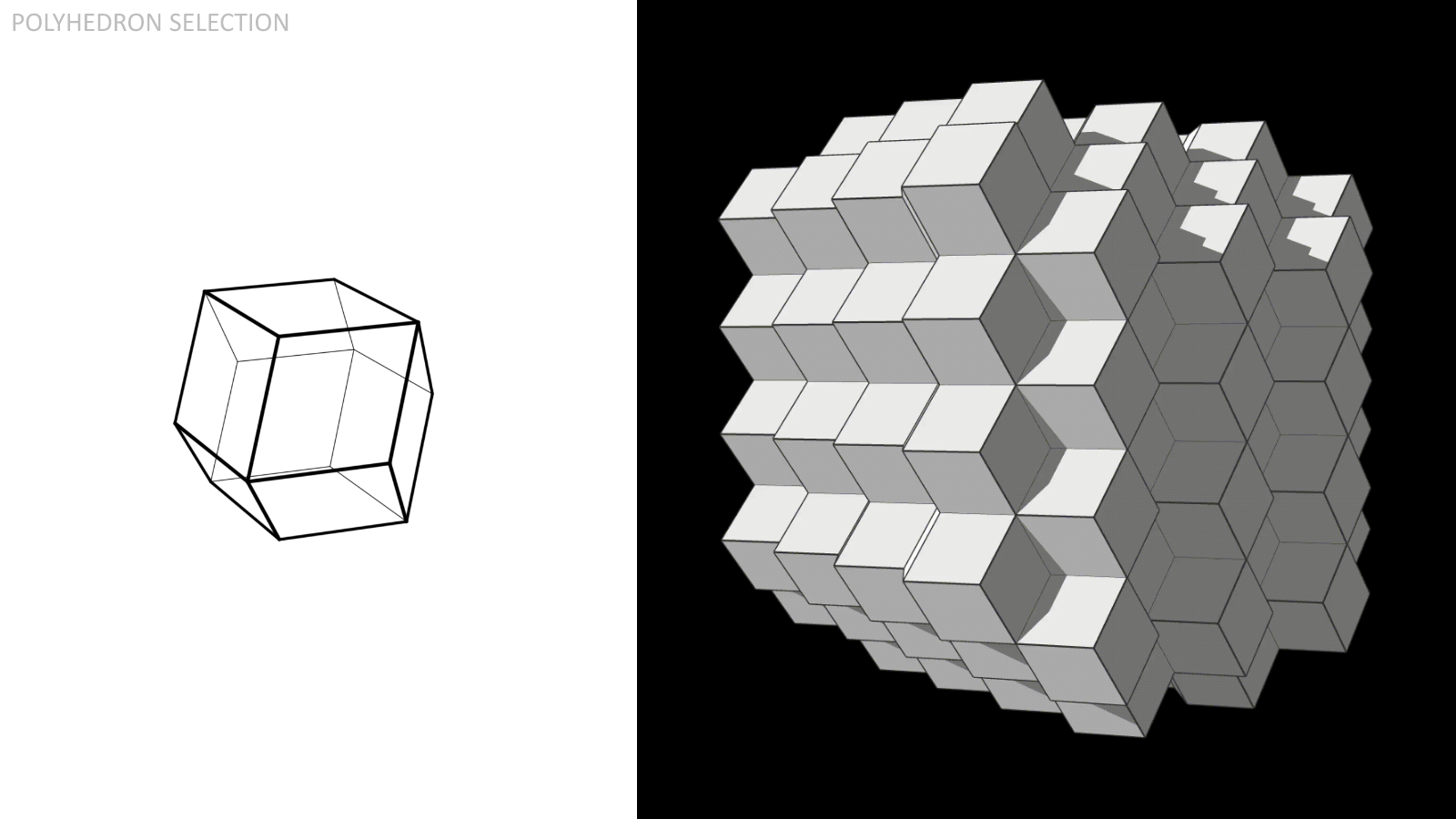
The Rhombic Dodecahedron, composed of (12) rhombi.

The Triangular Prism, composed of (2) regular triangles and (3) rectangles.

The Hexagonal Prism, composed of (2) regular hexagons and (6) rectangles. It's worth noting here that the proportions of these prisms were set to those that maximized Volume to Surface Area Ratio.

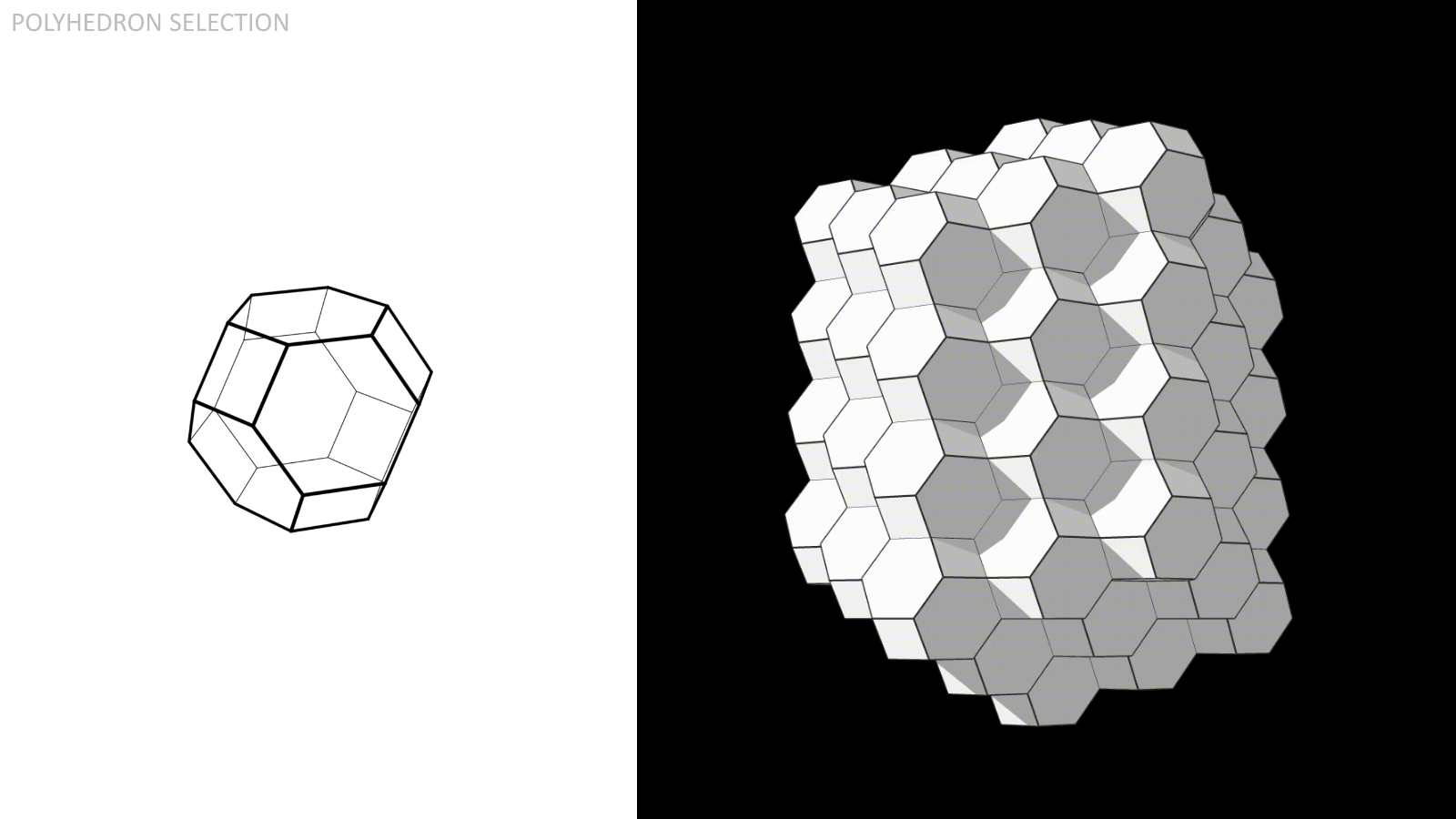
The Truncated Octahedron, composed of (8) regular hexagons and (6) squares.

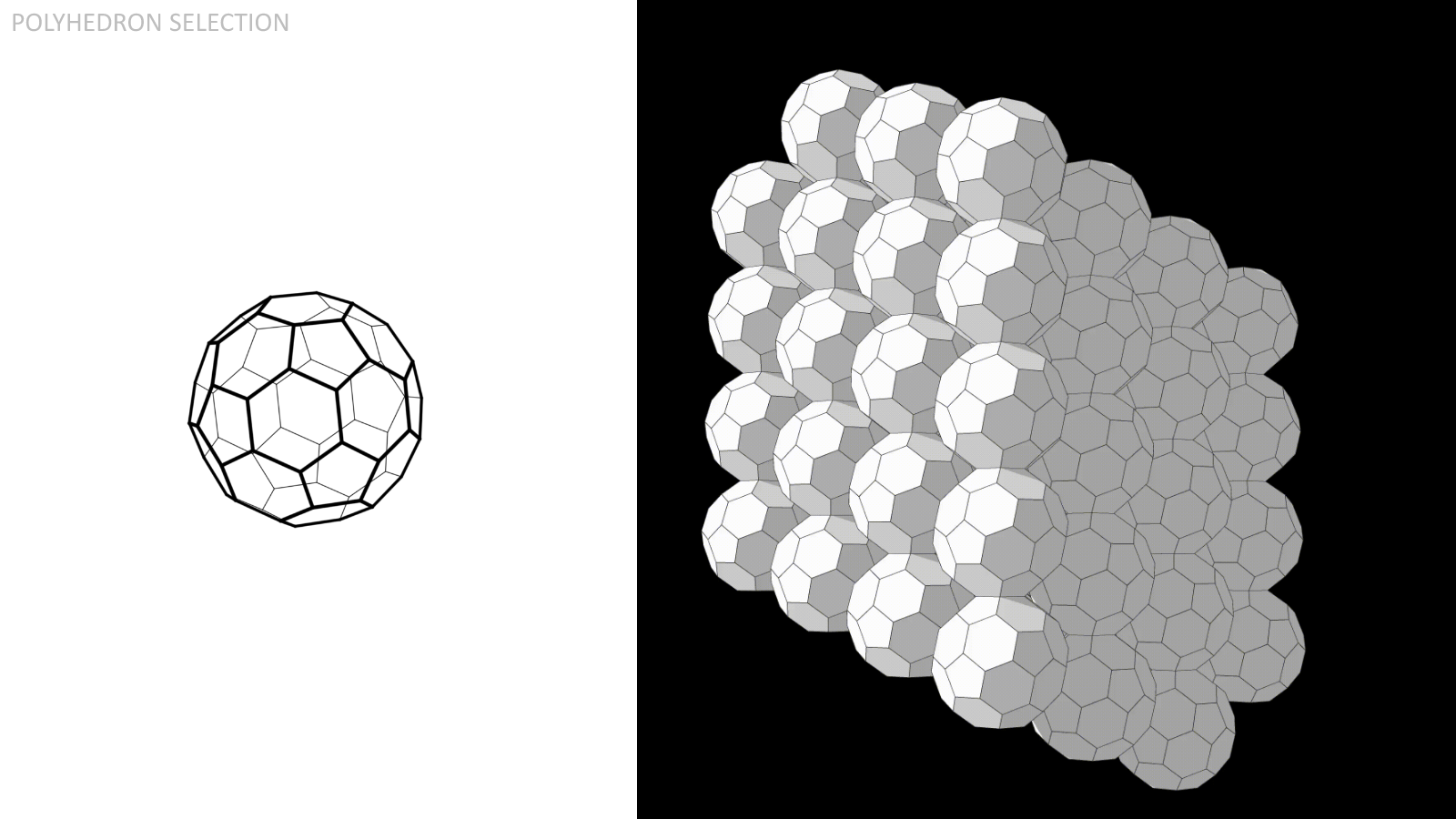
And finally the Truncated Icosahedron, composed of (20) regular hexagons and (12) regular pentagons.

So I've spoken about the selection of the candidate polyhedra, and now I'll explain the evaluation metrics. (14) were selected in total and I'll go through each of them now.

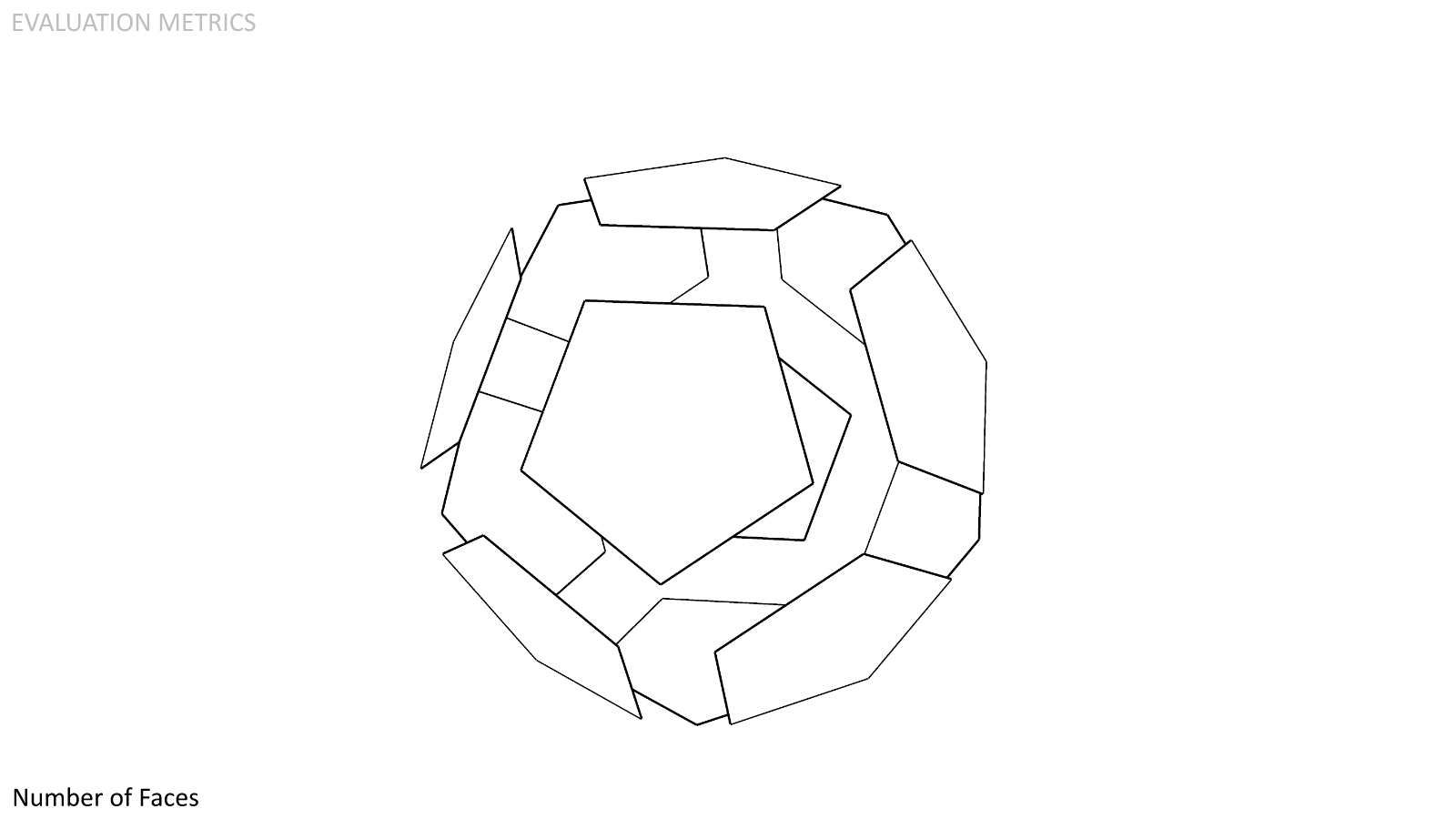
Number of Faces. Fewer faces means less complication in assembly and operation as well as fewer redundant systems.

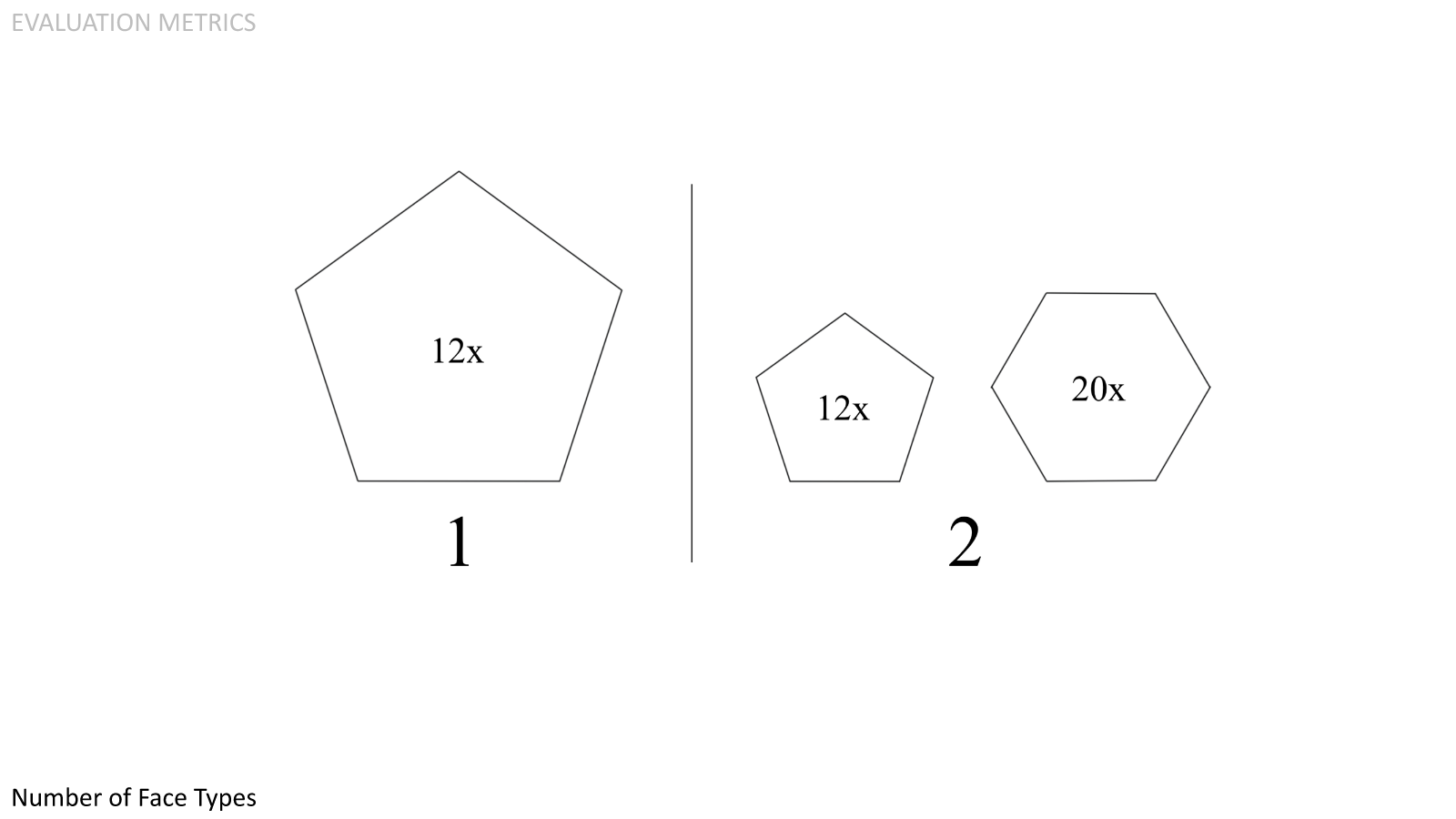
Number of Face Types. Fewer face types (ideally a single face type) means less engineering, fabrication, and qualification testing costs, as well as simpler deployment.

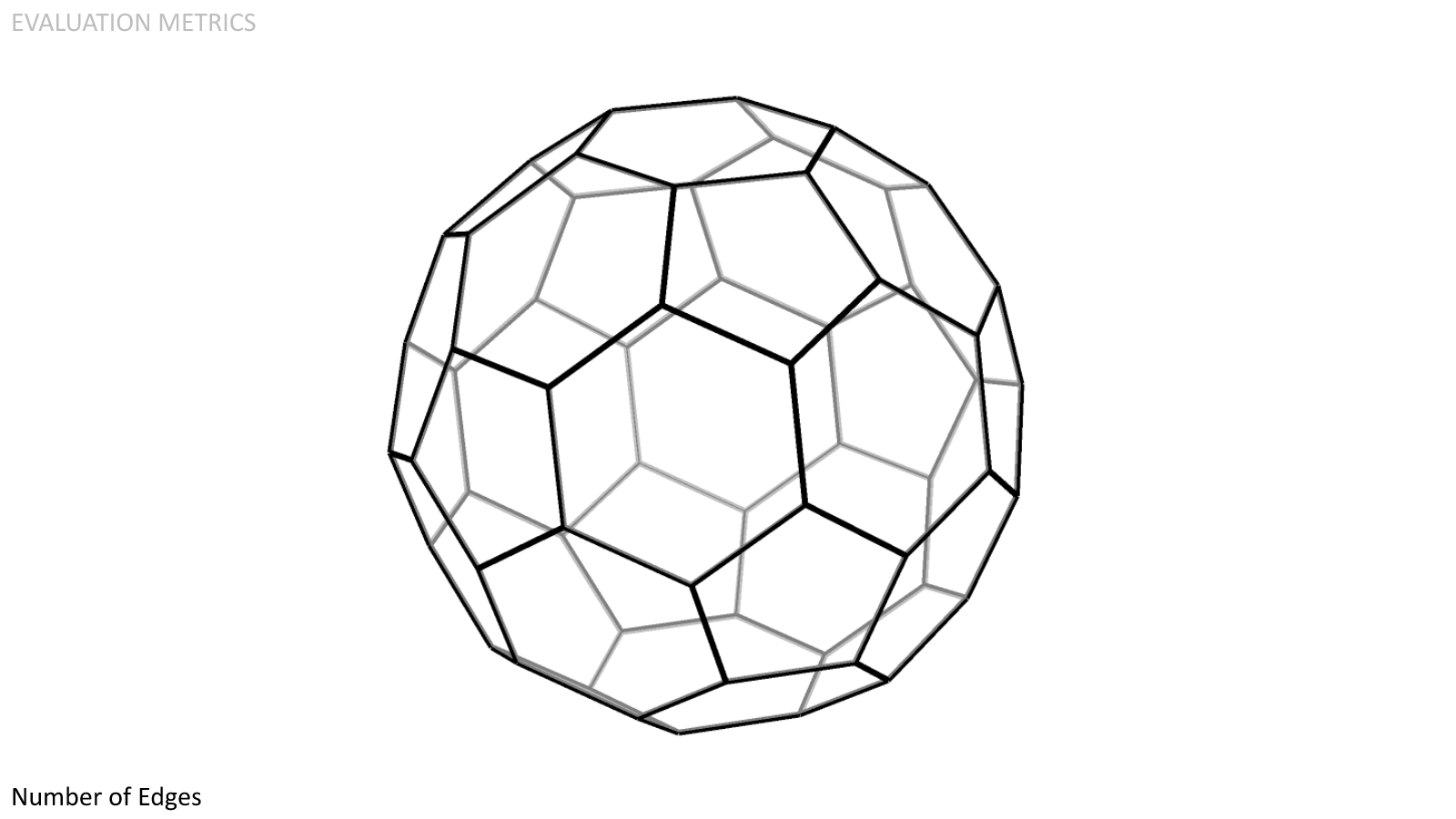
Number of Edges. Fewer edges simplifies the exchange of utilities as well as reduces the number of gaskets to vacuum.

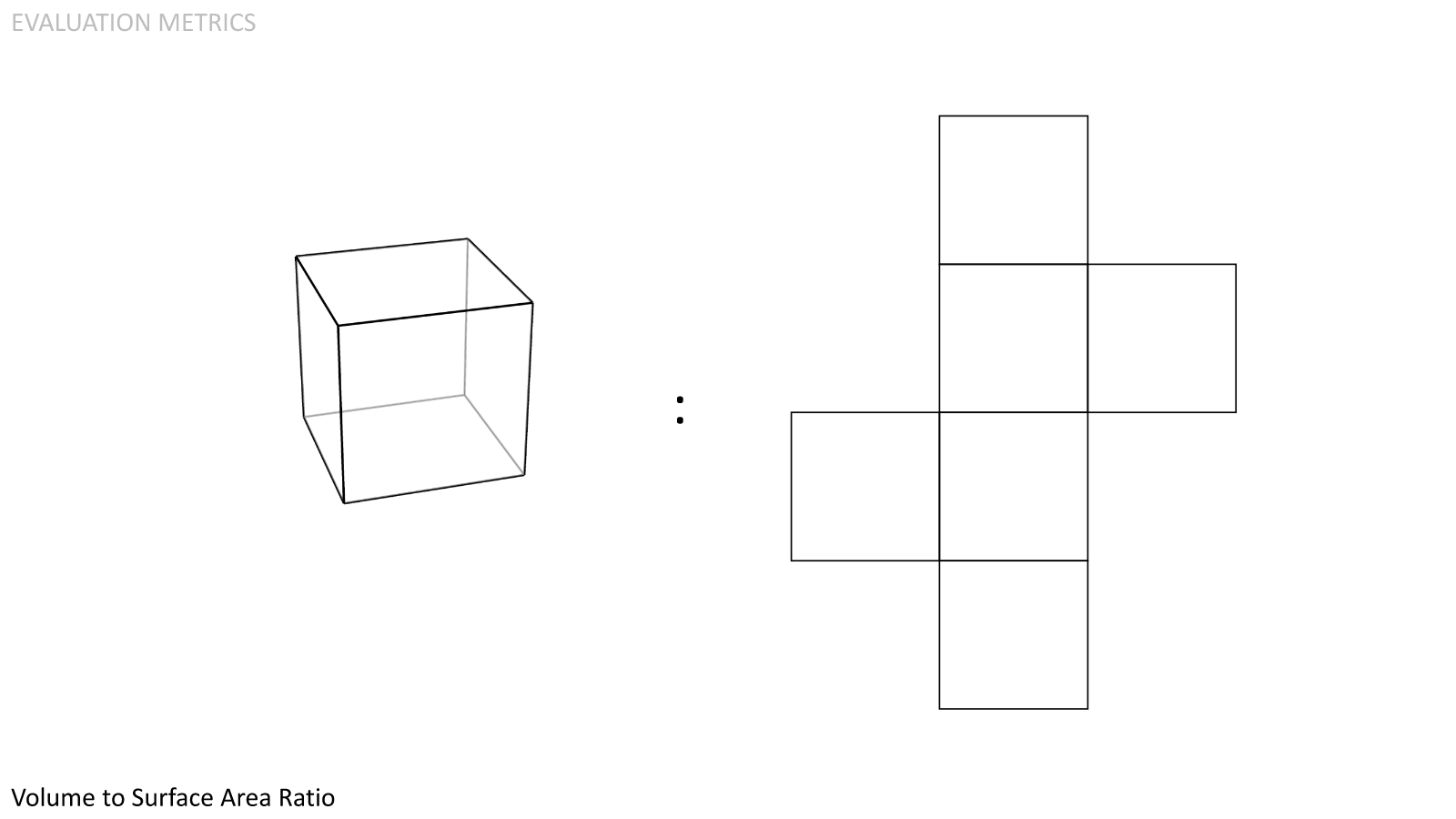
Volume to Surface Area Ratio. The greater the ratio, the more volume can be utilized per mass unit.

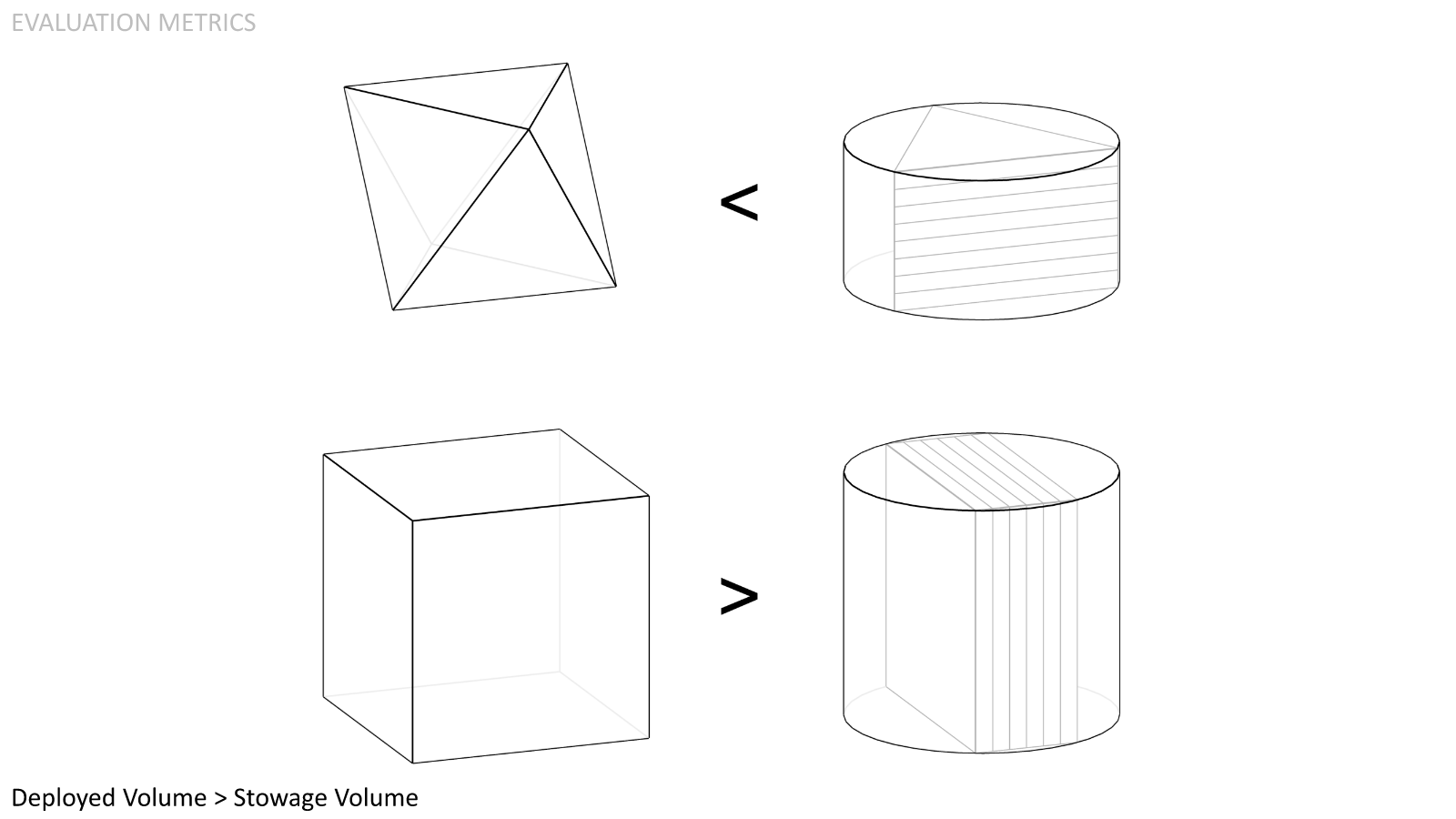
Deployed Volume Larger than Stowage Volume. Provided that the module faces are flat-packed, the deployed volume should be greater than the cylindrical volume required for stowage. Otherwise the benefit of on-orbit assembly is negated.

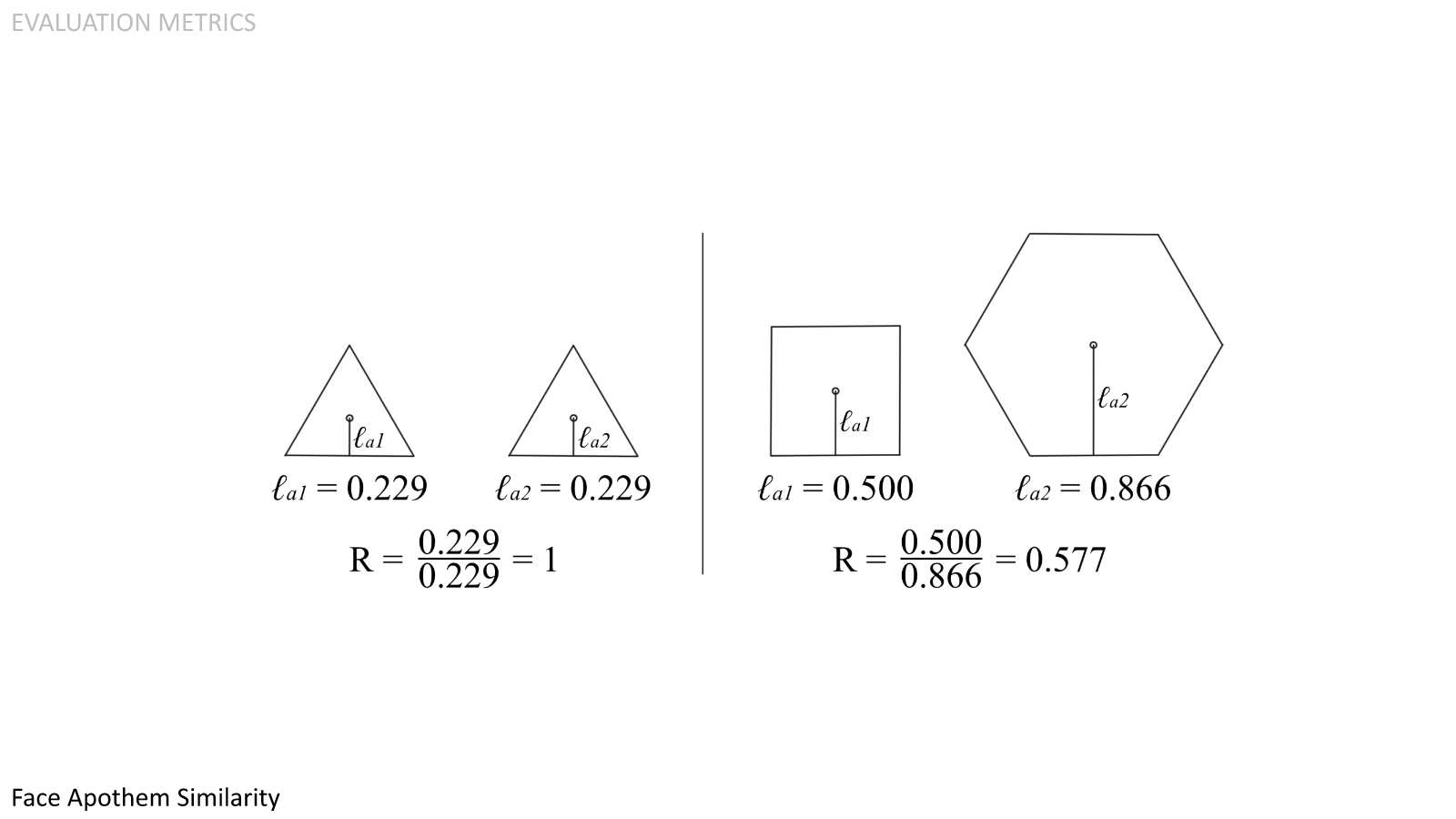
Face Apothem Similarity. Modular face panels will have many integrated systems. For polyhedra with more than one face type, it is advantageous for the sizes of the panels to be as similar as possible so as to efficiently utilize the area of each panel. The face apothem is a convenient shorthand for face size.

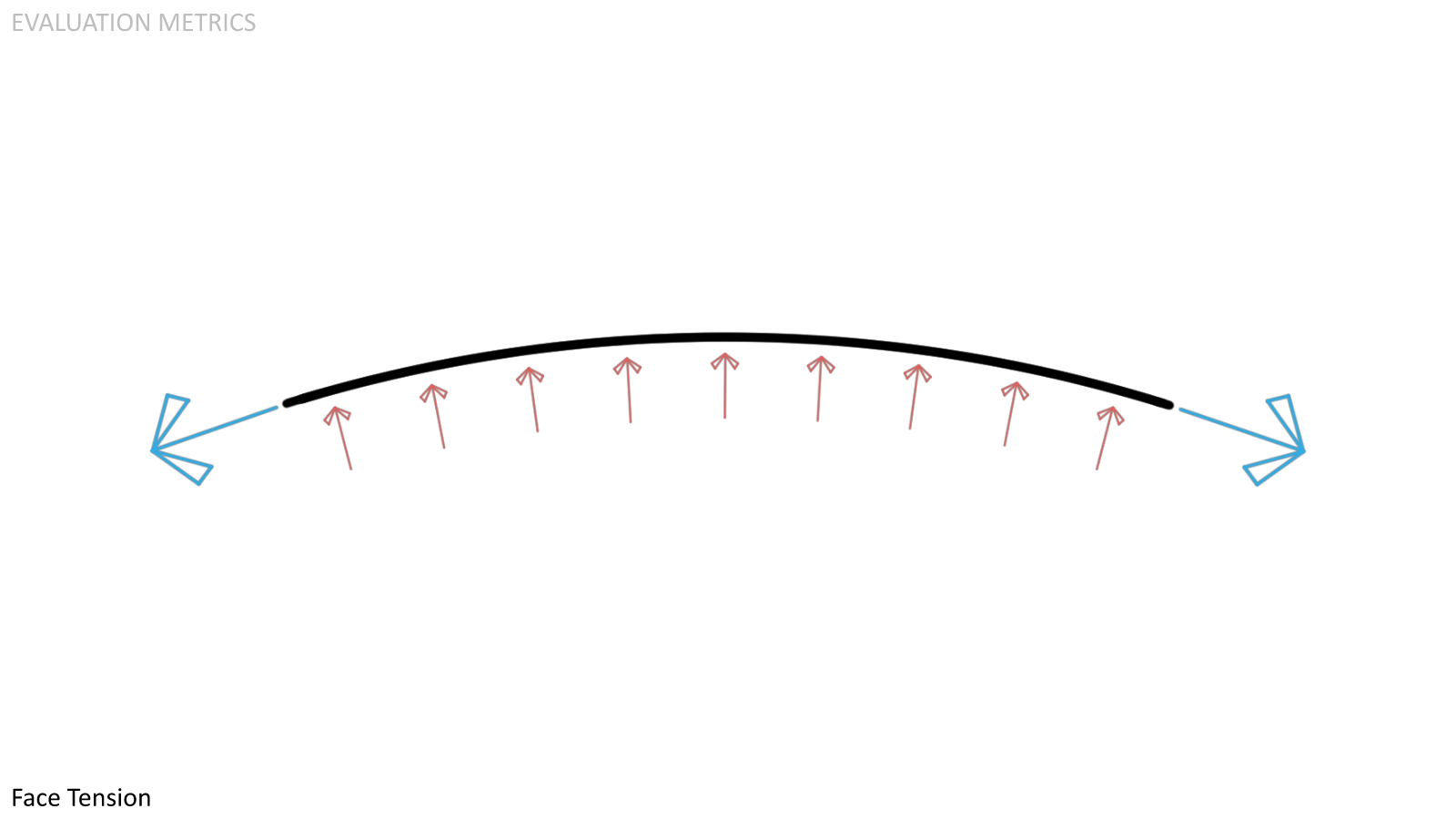
Face Tension. An internally pressurized surface will resolve the outward force through face tension. A lower face tension is advantageous as it means greater mass efficiency.

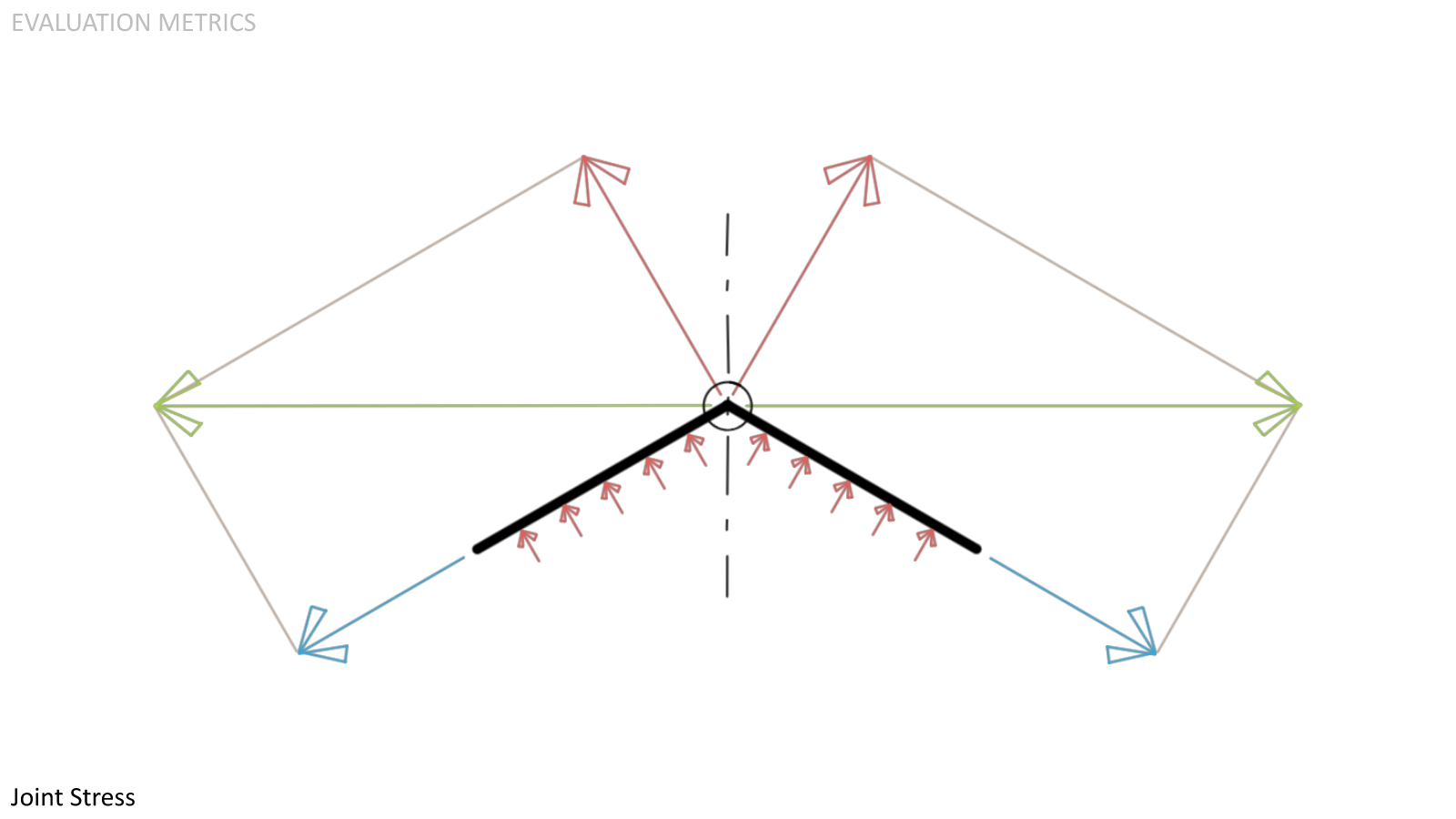
Joint Stress. Joints are a weak point in a polyhedral structure, but sustain the most stress in a pined face connection as the stress is the vector product of pressure reaction and the face tension. For the same reason as previously mentioned, a lower joint stress is advantageous.

Simulated Stress. Each polyhedron was modeled in Fusion 360 as hollow solids, they were internally pressurized, and the max stress was recorded. Again, the lower the stress, the better.

Space-Filling. I consider this one of the most important metrics. Space filling shapes allow for the following benefits:

- the complete utilization of three-dimensional space

- the reduction of exposure to radiation

- more connection possibilities and flexibility

- looping pathways instead of dead-end corridors

- structural rigidity

- the ability to contiguously enclose a volume of space

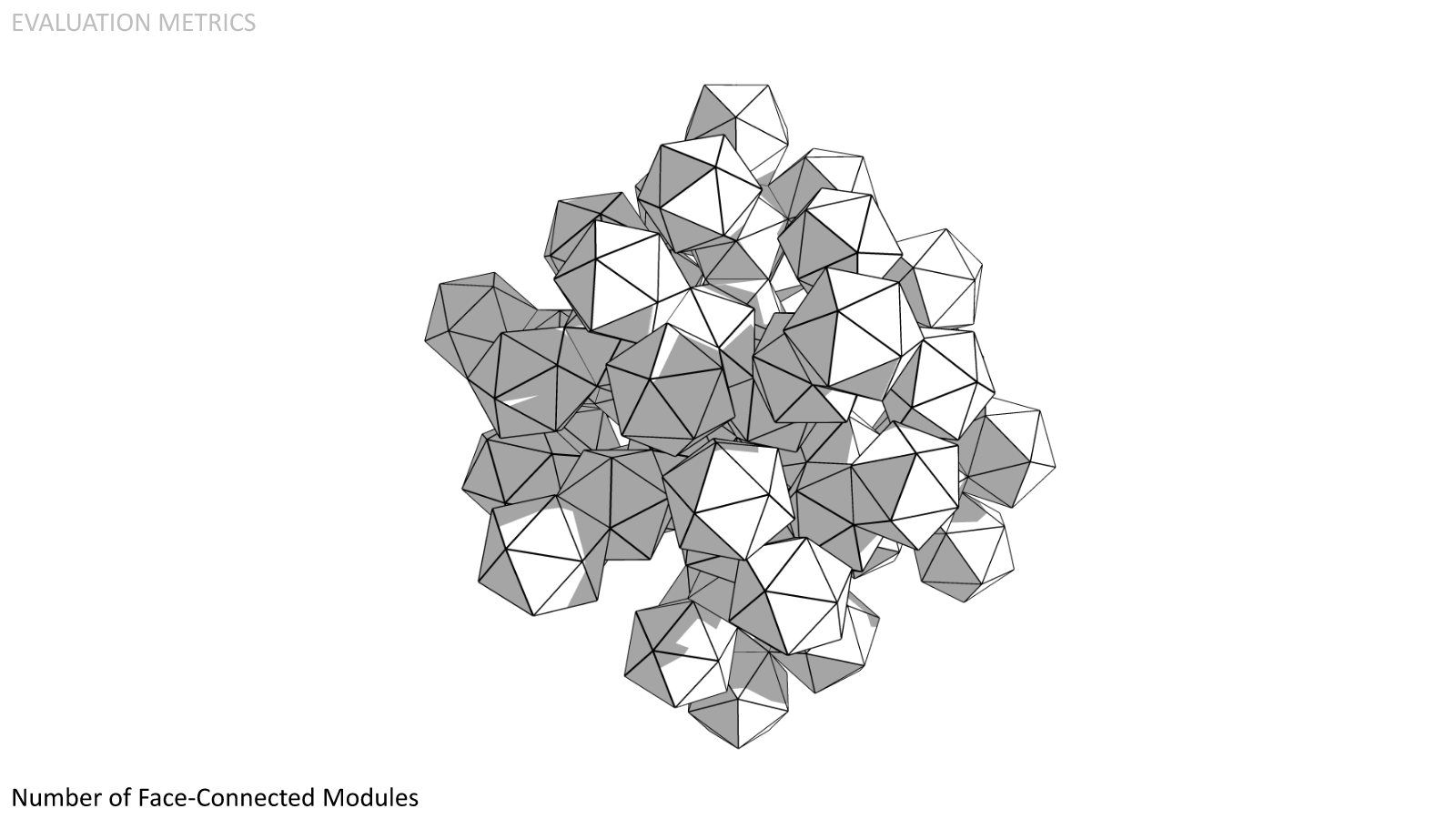
Number of Face-Connected Modules. It's advantageous to have a greater number of modules that can be connected to any given module. This increases the efficiency of both circulation and operations.

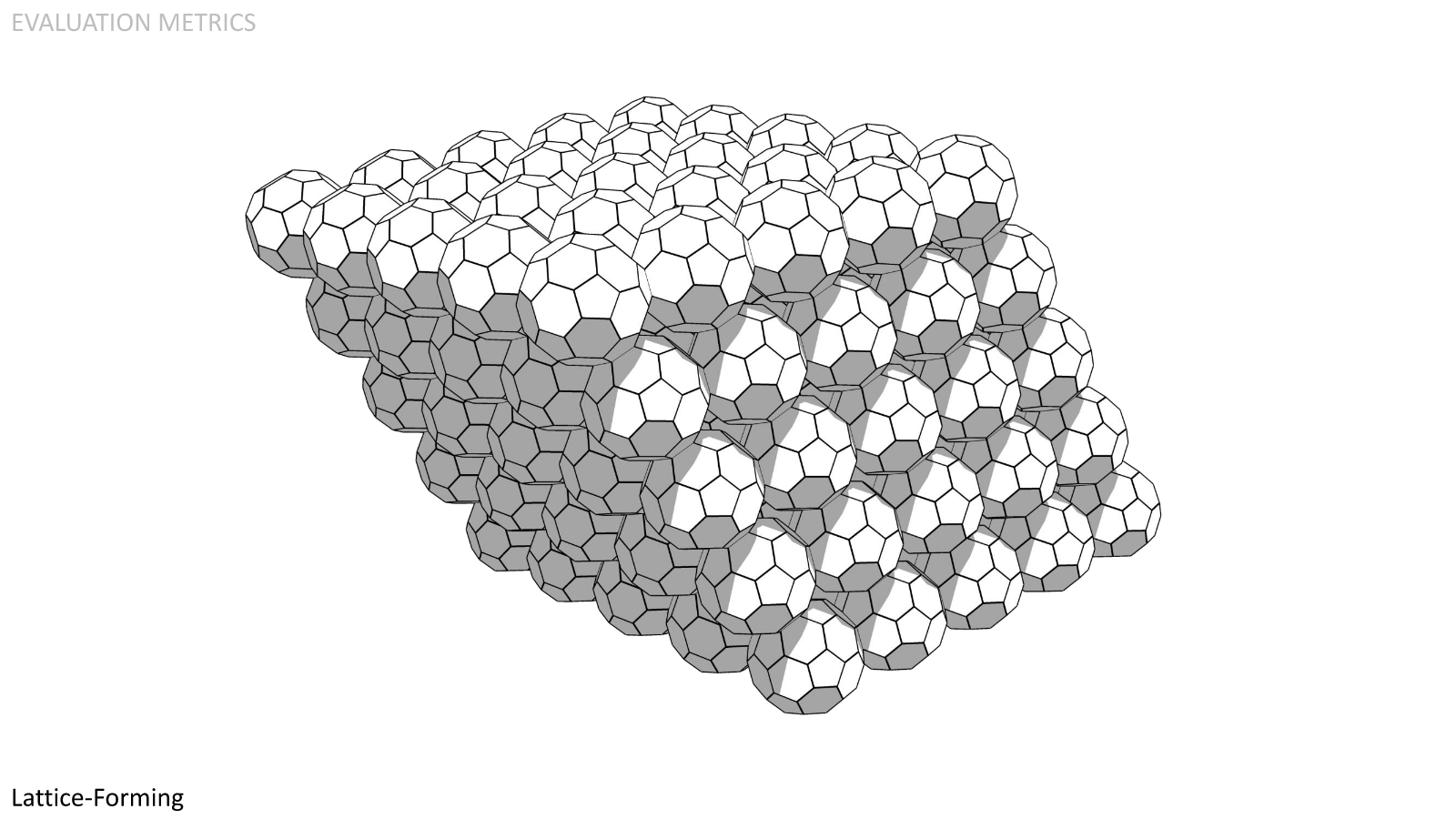
Lattice-Forming. Similar to Space-Filling, a lattice allows for looping pathways, better wayfinding, and structural rigidity.

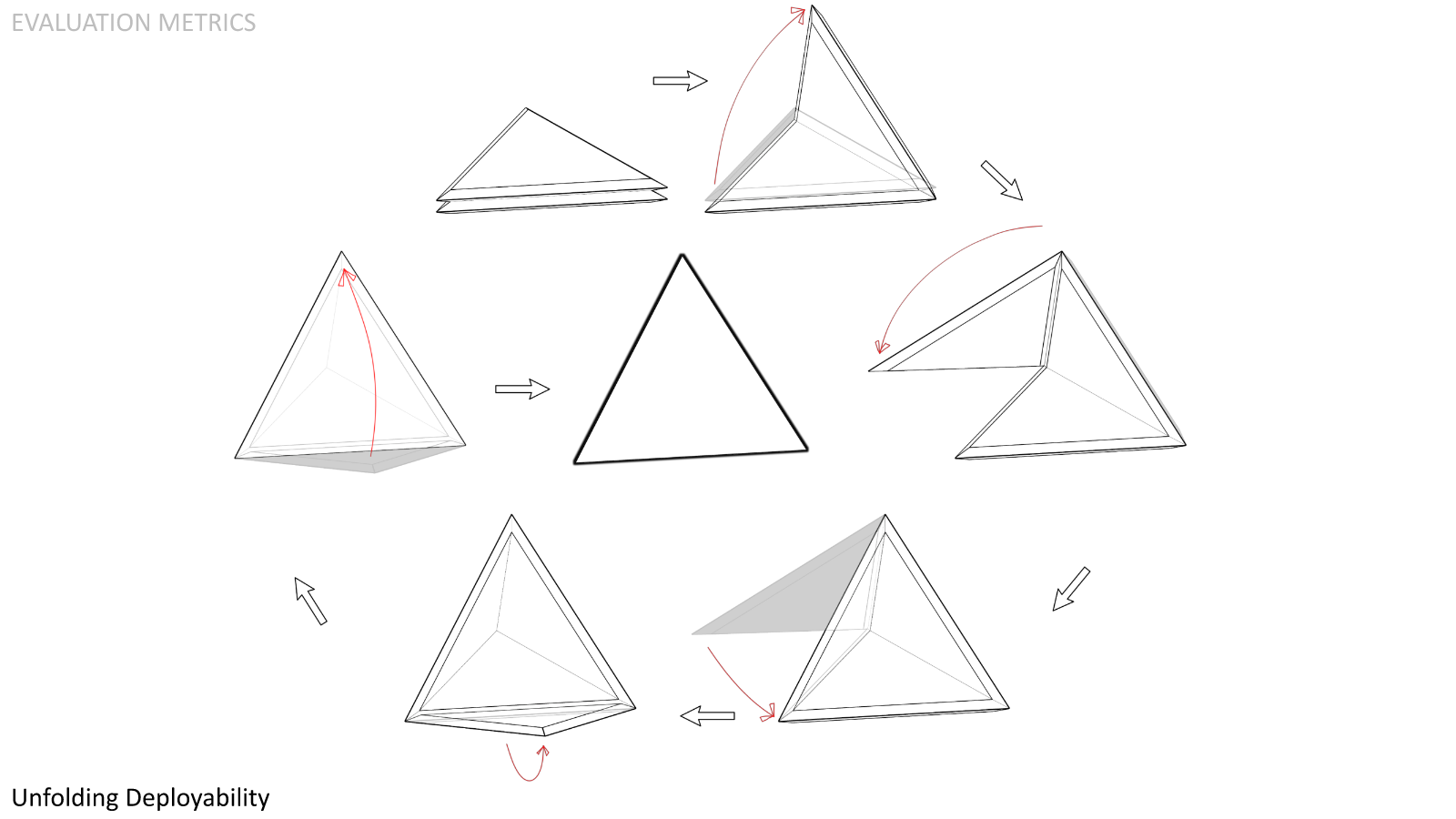
Unfolding Deployability. This is the ability for flat-packed panels to unfold along their edges until fully deployed. This capability maintains the connection of panels during assembly and eliminates the necessity for guidance systems to be integrated into each panel.

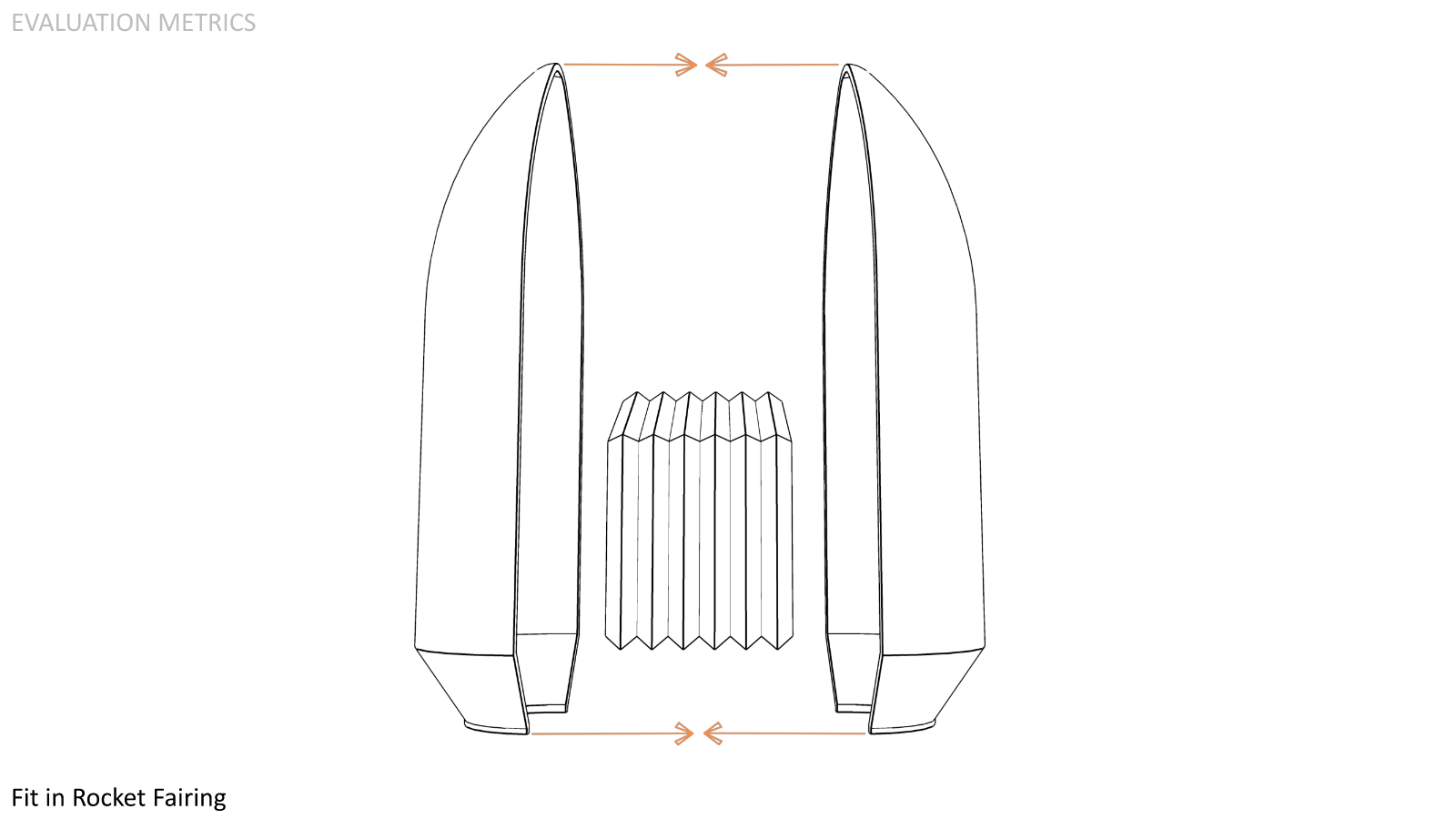
And finally,

Fit in Rocket Fairing. We can't necessarily rely on launch systems that are not currently operational. It's important that large modules are able to fit into currently operational launch vehicles.

So I've gone over the selection of candidate polyhedra and the evaluation metrics. Now I'll explain the analysis methodology.

The goal of the analysis is to take the raw values from the evaluation metrics (Number of Faces for example) and arrive at a best-performer. However there are three obstacles in the way:

- The raw values do not necessarily represent the performance of a given candidate compared to the others.

- The units between the evaluation metrics can be completely different and even of different magnitudes, which would be like comparing grapes to watermelons.

- Not all evaluation metrics are as important as every other, and some weighting likely needs to take place.

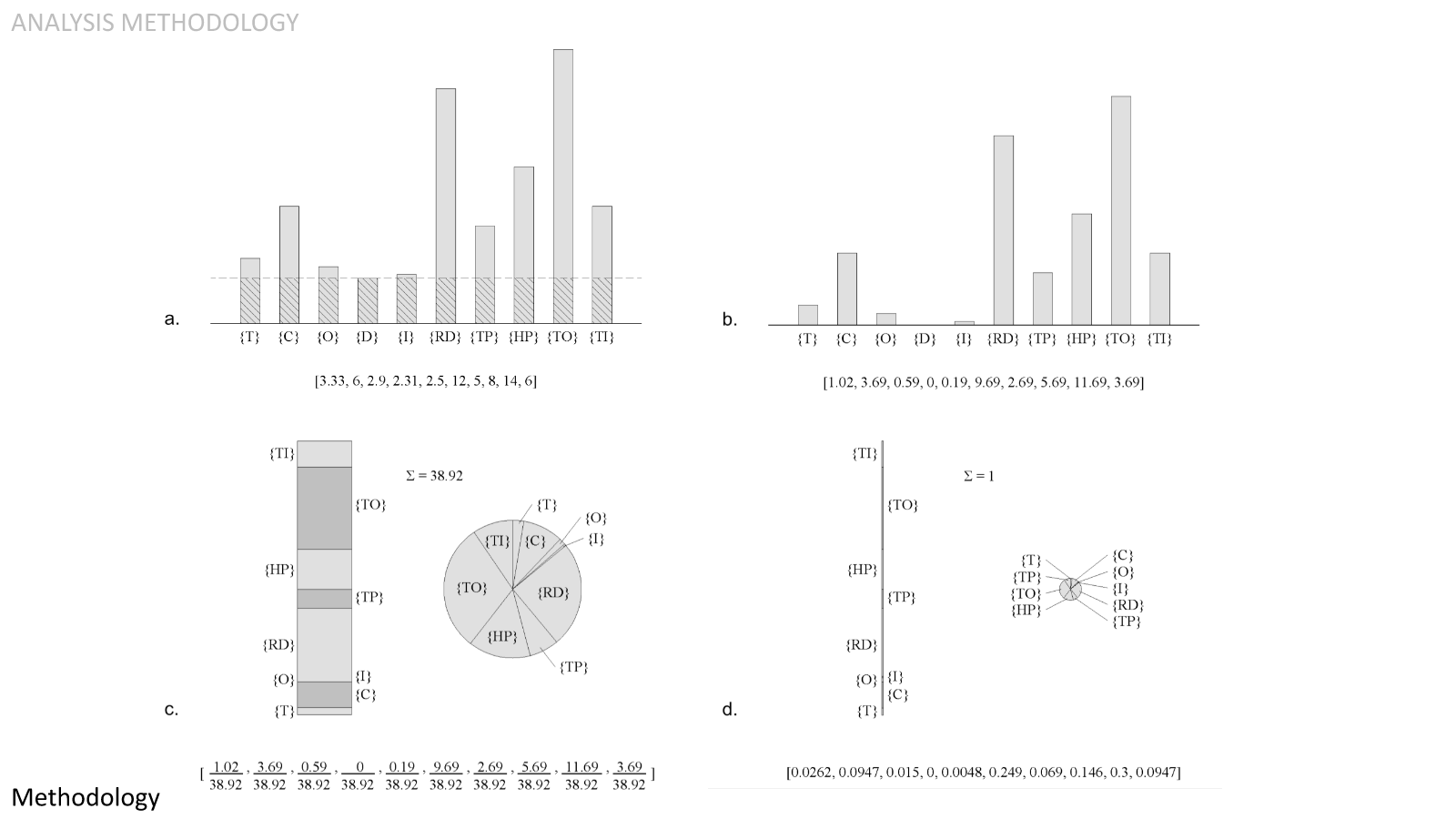
This graphic shows how the raw values were processed for each metric using a single metric as an example. In figure (a), we see the raw values for each of the candidates side-by-side. We find the poorest-performer and set that as the baseline. The differences between the raw values and the baseline are the performance values, shown in figure (b). This solves the performance disconnect. We can then add up all the performance values, shown in figure (c). We then divide each performance value by the sum of the performance values, which results in normalized performance values that can be seen in figure (d), where the sum of all the normalized performance values is one. This solves the issue of dissimilar units. This leaves the weighting, but we'll get to that in a moment.

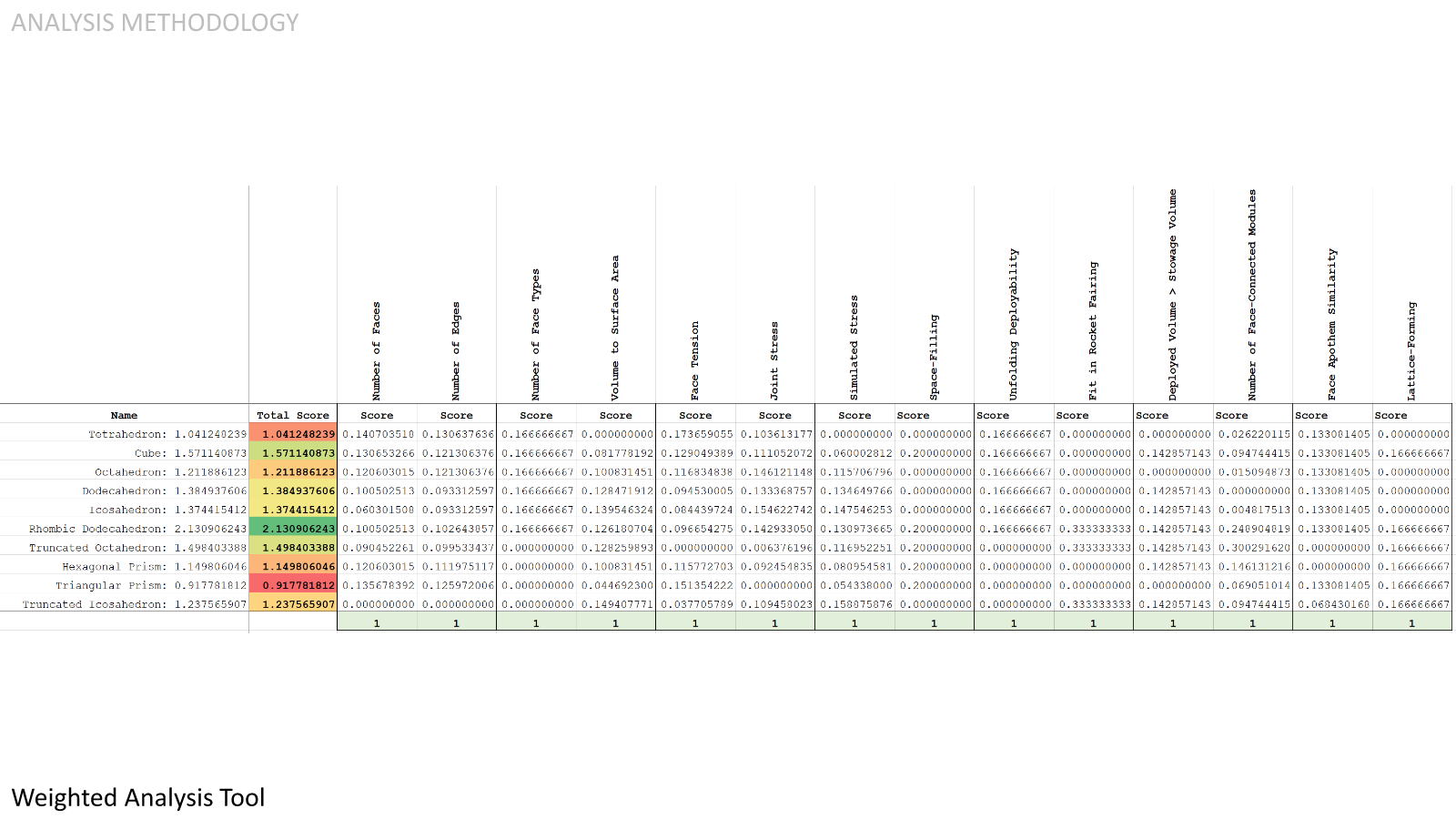
Using these normalized performance values, we can create a weighted analysis tool where we can input the normalized performance values for each evaluation metric, we can add weights to these evaluation metrics, and it will output a final score. But which weights should we choose? Without knowing how every weight would turn out, it's impossible to objectively determine how each candidate polyhedron stacks up against each other.

So I wrote a Python script to test all the combinations of importance levels up to (5) levels of importance; this took nearly (6) days to run. Some of you might ask, "why not (6) levels of importance?" And to that I say, an analysis of (6) levels would have taken about (70) days to run, so please forgive me.

I was expecting a descending distribution wherein I could analyze under which circumstances different polyhedra would perform best, but that is not at all what came out of this analysis.

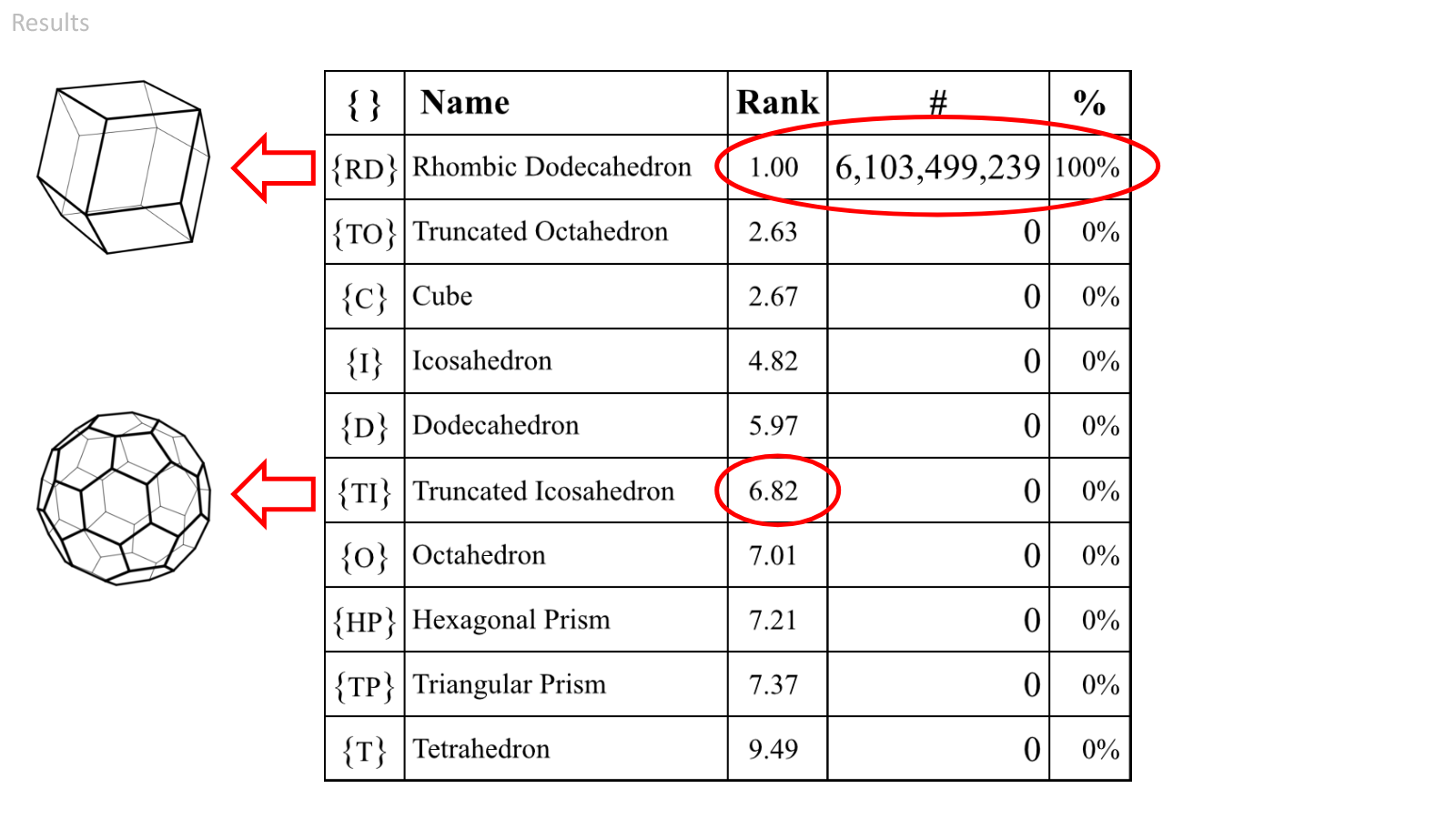
This table shows the candidate polyhedra along with their average ranking, the number of times the polyhedra were ranked first, and the percent of total combinations where the polyhedra were ranked first.

If it's not immediately obvious, I'll call your attention to these figures here. In every single one of the 6.1 billion combinations of importance factor weights, the Rhombic Dodecahedron ranked first. This means that no matter which weights one might put on each of the evaluation metrics (at least to an importance level of 5), the Rhombic Dodecahedron will remain on top.

The Truncated Icosahedron, the polyhedron with the largest Volume to Surface Area Ratio is ranked 6th.

I conclude that the Rhombic Dodecahedron should be considered the default for any prospective polyhedral space habitat module design. Furthermore, I propose that the Truncated Icosahedron should be deprioritized from consideration for the same.

With that, I'll say that I'm honored to have had the opportunity to speak here at the IAC and I look forward to meeting with you all and sharing ideas over the course of this week.