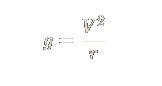Simulating Gravity with Rotational Acceleration

Gravity

Gravity is a force that acts on mass-energy at a distance by way of bending spacetime. This force can be described using the mass of the two objects (M), the distance between the object's centers of mass (r), and the gravitational constant (G):

The gravitational acceleration on Earth (g) is derived by this using the gravitational constant (G), the mass of Earth (M), and the radius of the Earth (r):

Rotational Acceleration

A rotating space habitat simulates the experience of gravity by way of centripetal force. Objects on the inside surface of the rotating shell of the habitat are constantly acted upon perpendicularly to their tangential velocity. A given gravitational acceleration (g) can be simulated by adjusting the radius (r) of the rotating shell and/or the velocity of the shell (V):

There are several practical differences between gravitational acceleration and rotational acceleration that affect the experience of the individuals inhabiting them.

Height Changes Acceleration

Since gravity is a relatively weak force compared to the other fundamental forces, the radius at which it induces standard gravity using ordinary solid mass is necessarily large (the radius of the Earth for example) compared to the size of individuals. By contrast, rotating habitats can induce the same acceleration (A) with a much smaller radius (r) by spinning at the required velocity (V) for that radius.

This radius can be small enough that the radius is not too much larger than the occupants. When this happens there is a perceptible acceleration gradient on the individuals.

For a rotating shell that has a radius of 100 meters, a 1% difference in simulated gravity (9.7 vs 9.8) will be perceived at 1 meter from the surface of the shell. 1% at 1 meter may not seem like a lot, but consider that this effect increases with any change of height in the structure. If there are 2 or 3 levels, then this effect is increased when individuals travel in an elevator or ascend a flight of stairs. A 3-level shell in this scenario has the potential to create a ±4% difference in the simulation of gravity depending of which level one is on.

This acceleration gradient can be quite disorienting, especially when standing up or sitting down. This is the phenomenon that has lead researchers to recommend habitats rotate at 2 RPM at the most for simulating 1 g.

Movement Changes Acceleration

The centripetal force on an object is determined by rotation rate and radius only for static objects relative to a point on the circumference. If an object is traveling along the circumference, then the centripetal force will change as the effective rotational velocity has has either increased or decreased (depending on if the body is travelling spinward or anti-spinward). If the body is moving in the spinward direction the centripetal force will increase (Vo=V1+V2), while if the body is moving in the anti-spinward direction the centripetal force will decrease (Vo=V1-V2). In fact, if a body moves in the anti-spinward direction at the same speed as the shell is rotating, then there will be no centripetal force on the body and it will experience weightlessness (Vo=V1-V1 => Vo=0).

In very large structures, this is not normally an issue for inhabitants, but this effect becomes more important for smaller rotating shells. For rotating shells simulating standard gravity, the typical running speed for physically active humans in a 100 meter radius shell can change the effective simulated gravity they experience by ±38% and in a 300 meter radius shell the effect is still ±21%. In fact, the effect does not drop to ±1% until the shell exceeds 124 kilometers in radius.

Most solutions for offering different levels of gravity simulation assume that offering different levels of simulated gravity must be accomplished by way of building shells at different radii, but the same effect can be accomplished by a compartment that moves at a different speed along the circumference.

Floating and Flying

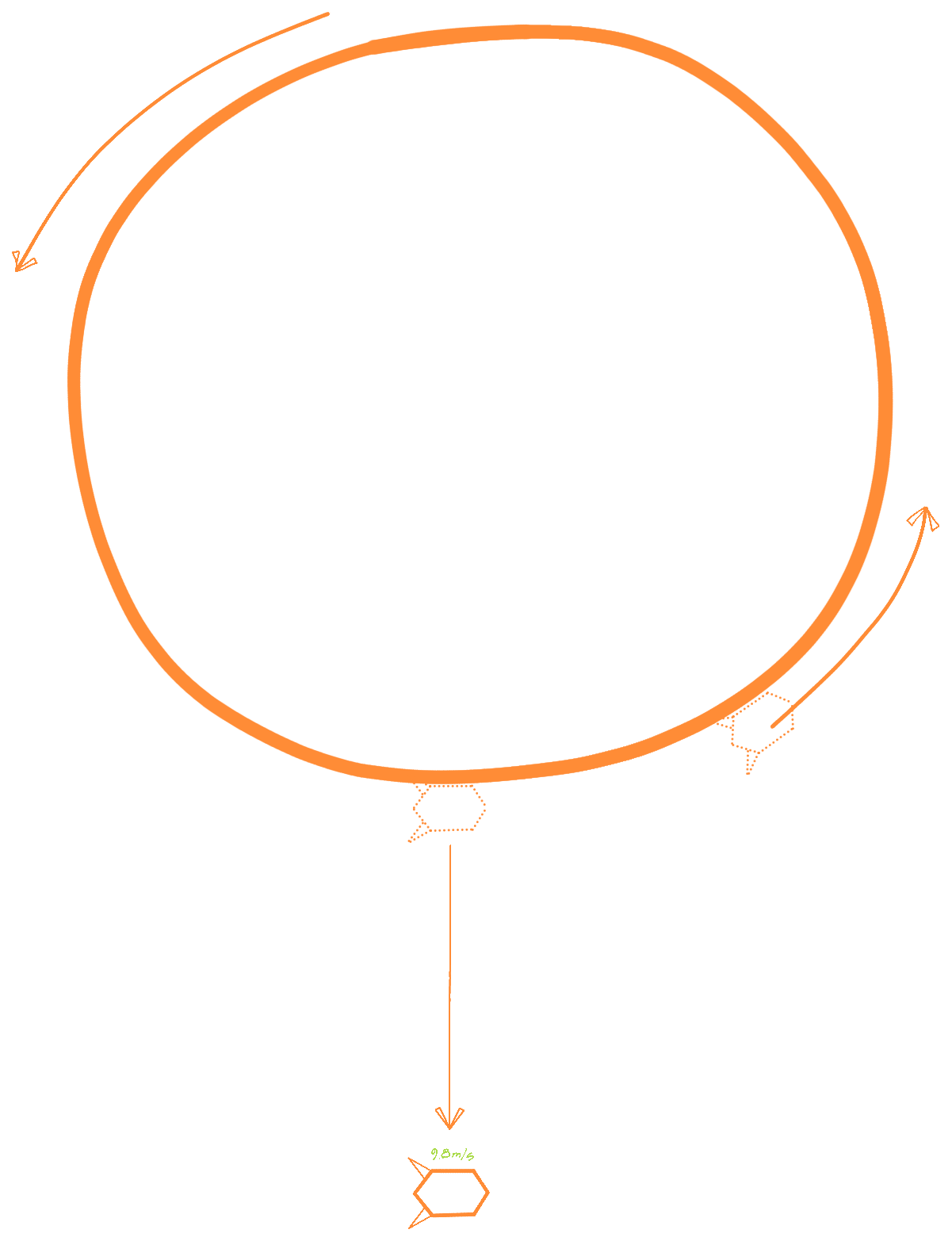
Since rotational acceleration only acts on objects in contact with the rotating shell (as opposed to at a distance as is the case with gravity), objects can "hover" over the interior surface of a rotating shell as long as the object is not moving with respect to the axis. To observers on the rotating surface of the shell, the aforementioned object will appear to be flying through the air at the same speed at which the shell is rotating.

If the rotating habitat is an air-filled drum, the center of the drum is an area where individuals can float and or fly around under their own power. The further from the center these individuals travel, the greater force the slowly rotating air will exert on them. If not corrected, any object in the center of the drum will eventually be moved enough that it gets blown into the surface of the shell, which will most-likely result in the object colliding with another object travelling at the speed of rotation.

Rotating Away

When in a rotating shell, the "floor" is constantly reorienting the individual. If the individual were to jump (thus breaking the connection), the shell would effectively bend out from underneath them slightly in the spinward direction before they connected with the floor again. This effect is greater when either the jump is higher or when the shell radius is smaller. When the effect is great enough, individuals may find that even though they may have jumped straight "up", they fall "down" on their face or back.

Escape

It's likely no surprise to the reader that Earth is a gravity well. There is a high energy cost to escaping this gravity well. This is evident when reviewing the amount of fuel as a percentage of total mass for current space vehicles/propellants, which can be anywhere from 83%-96%*. This represents a great amount of energy.

By contrast, a rotating space habitat has no gravity well. If escape is desired, a vehicle need only detach itself from the side or exterior of the habitat. Once released, the vehicle will travel with the velocity it had at time of release, which would be roughly 9.8 m/s in the "downward" direction (tracing the line that connects the axis to the point of release) assuming the structure is simulating Earth normal gravity*. In this way, the escape trajectory can be tailored by releasing the vehicle at a calculated moment. Additionally, if the vehicle is able to travel along the exterior of the circumference of the habitat, the escape velocity of the vehicle can be tuned to be lower or higher.

*Thanks to reddit user u/Le_German_Face for pointing out an error in the original publication, which has since been fixed.